Data Structures

Introduction

This is Data Structures tutorial from YouTube. I will learn it step by step.

Content

Course list

I grab the html contents from source page, and use regular expression to parse it.
(?<=aria-label\=").*?(?=by\smycodeschool)

Introduction to data structures

A data structure is a way to store and organize data in a computer, so that it can be used efficiently.
We talk about data structures as:

Mathematical/Logical models, we defined them from abstract view, that is Abstract data types (ADT).
Implementation, concrete data types
ADT is to define data and operations, but no implementation, e.g. arrays, linked list, stack, queue, tree, graph and so on.

We will study it from the following four aspects:

logical view
operations (available to us)
cost of operations (time)
implementation (in the programming language)

List as ADT

List is nothing but a collection of objects of the same type. It is generally a fixed-size list, if the current list is full, you should create a bigger-size list to contain many elements.
Here, we mainly talk about the time complexity of list operations.

Access - Read or write element at an index, constant time $O(1)$
Insert - depend on the list length, $O(n)$
Remove - $O(n)$
Add - $O(n)$

linked list

For array created using “malloc” function in C (dynamic memory allocation), we can use “realloc” function to re-size it. Same memory block may be extended if space adjacent to the block is available. Else, a new block is created.
head, the address of the head node gives us access of the complete list.
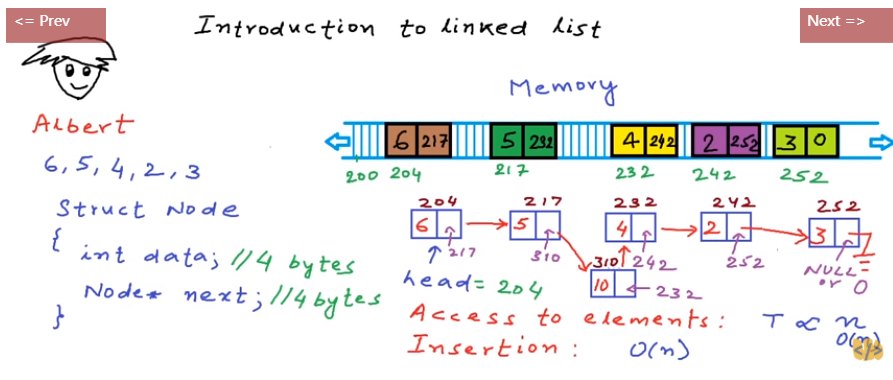Time complexity:

Access to elements: $O(n)$
Insert: $O(n)$
Delete: $O(n)$

array vs linked list

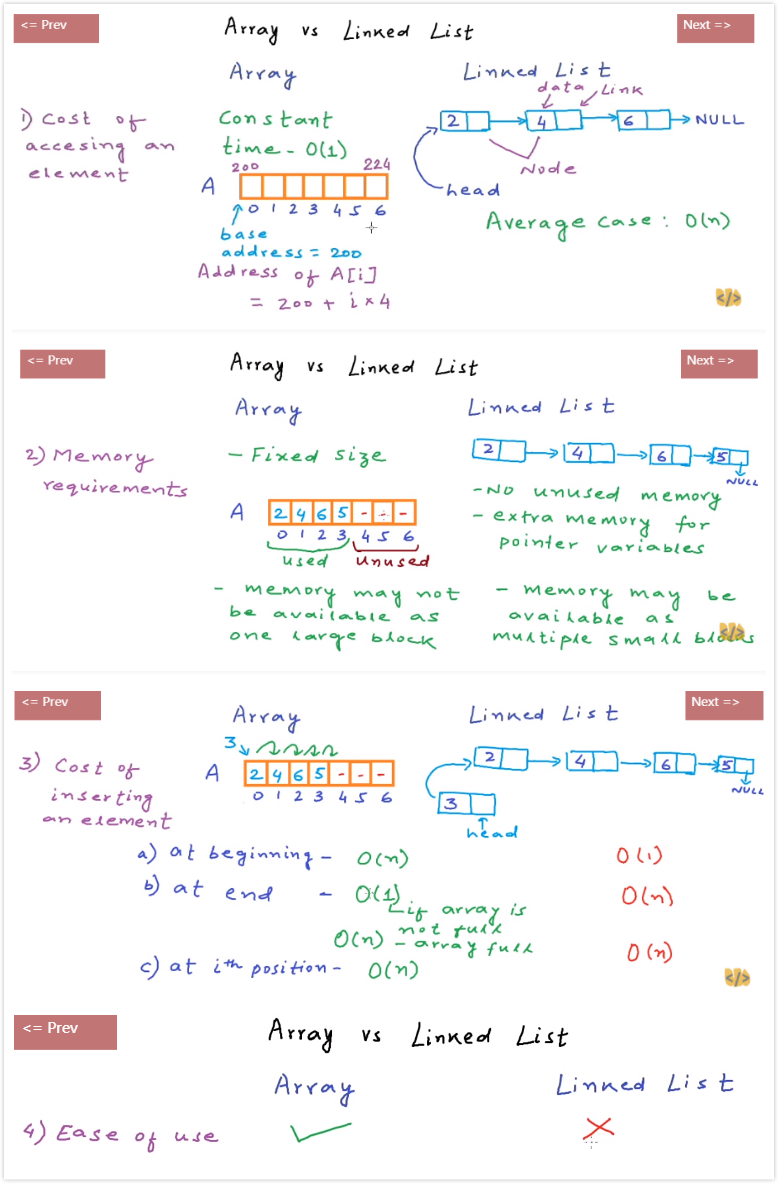
Cost of accessing an element

For array, it provides a base address (head address), and array is stored in the contiguous manner. So given an array A for accessing t-th element, it just calculate the result of base address + i *sizeof(array_data_type); time complexity: $O(1)$

For linked list, because it is a ordered list, we have to start with head node. So, it is kind of like traversing. time complexity: $O(n)$
Memory requirements

For array, it is fixed size and memory may not be available as one large block

For linked list, it has no unused memory and it has extra memory for pointer variables. Memory may be available as multiple small blocks

Cost of inserting (deleting) an element

cases	Array	Linked list
at beginning	$O(n)$	$O(1)$
at end	array is not full: $O(1)$	$O(n)$
	array is full: $O(n)$
at i-th position	$O(n)$	$O(n)$

Ease of use (implementation)

For array, it is easy.

For linked list, it may be difficult for C/C++. It may cause segmentation fault or memory leak.

lined list implementation

#include<iostream>

struct Node
{
	int data;
	Node* next;
};

class LinkedList
{
private:
	Node *head, *tail;
public:
	LinkedList() 
	{
		head = NULL;
		tail = NULL;
	}

	void CreateNode(int value)
	{
		Node* temp = new Node;
		temp->data = value;
		temp->next = NULL;

		if (head == NULL) 
		{
			head = temp;
			tail = temp;
			temp = NULL;
		}

		else  
		{
			tail->next = temp;
			tail = temp;
		}
	}
	void Display()
	{
		Node* temp = new Node;
		temp = head;
		while (temp != NULL)
		{
			std::cout << temp->data << "\t";
			temp = temp->next;
		}
		std::cout << "\n==================================================\n";
	}
	void Insert_start(int value)
	{
		Node* temp = new Node;
		temp->data = value;
		temp->next = head;
		head = temp;
	}
	void Insert_end(int value)  
	{
		Node* temp = new Node;
		temp->data = value;
		temp->next = NULL;
		tail->next = temp;
		tail = temp;
	}
	void Insert_position(int value, int pos)
	{
		Node* temp = new Node;	
		Node* pre = new Node;	
		Node* cur = new Node;	

		cur = head;
		for (int i = 0; i < pos; i++)
		{
			pre = cur;
			cur = cur->next;
		}
		temp->data = value;
		pre->next = temp;
		temp->next = cur;
	}
	void Delete_start()
	{
		Node* temp = new Node;
		temp = head;
		head = head->next;
		delete temp;
	}
	void Delete_end()
	{
		Node* cur = new Node;
		Node* pre = new Node;

		cur = head;
		while (cur->next != NULL)
		{
			pre = cur;
			cur = cur->next; 
		}
		tail = pre;
		pre->next = NULL;
		delete cur;
	}
	void Delete_position(int pos)
	{
		Node* cur = new Node;
		Node* left = new Node;

		cur = head;
		for (int i = 0; i < pos; i++)
		{
			left = cur;
			cur = cur->next;
		}
		left->next = cur->next;
	}
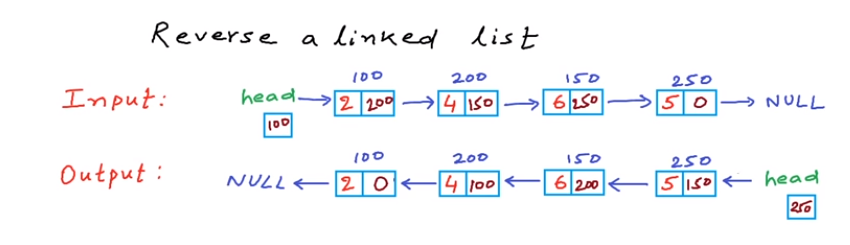
	void Reverse()
	{
		Node* cur = new Node;
		Node* left = new Node;
		Node* right = new Node;

		left = NULL;
		right = NULL;
		cur = head;
		while (cur != NULL)
		{
			right = cur->next;
			cur->next = left;
			left = cur;
			cur = right;
		}
		head = left;
	}

};

int main()
{
	LinkedList ll;
	int values[4] = { 25,50,90,40 };
	for (int value : values)
	{
		ll.CreateNode(value);
	}
	std::cout << "===========create a list==========================\n";
	ll.Display();

	std::cout << "==========Insert at beginning=====================\n";
	ll.Insert_start(36);
	ll.Display();

	std::cout << "==========Insert at end===========================\n";
	ll.Insert_end(73);
	ll.Display();

	std::cout << "==========Insert at 2-th position=================\n";
	ll.Insert_position(98, 2);
	ll.Display();

	std::cout << "==========Delete start============================\n";
	ll.Delete_start();
	ll.Display();

	std::cout << "==========Delete end==============================\n";
	ll.Delete_end();
	ll.Display();

	std::cout << "==========Delete at 2-th position=================\n";
	ll.Delete_position(2);
	ll.Display();

	std::cout << "==========Reverse linked list=====================\n";
	ll.Reverse();
	ll.Display();

	std::cin.get();
}

results:

===========create a list==========================
25      50      90      40
==================================================
==========Insert at beginning=====================
36      25      50      90      40
==================================================
==========Insert at end===========================
36      25      50      90      40      73
==================================================
==========Insert at 2-th position=================
36      25      98      50      90      40      73
==================================================
==========Delete start============================
25      98      50      90      40      73
==================================================
==========Delete end==============================
25      98      50      90      40
==================================================
==========Delete at 2-th position=================
25      98      90      40
==================================================
==========Reverse linked list=====================
40      90      98      25
==================================================

Iterative Reverse
Recursive Reverse

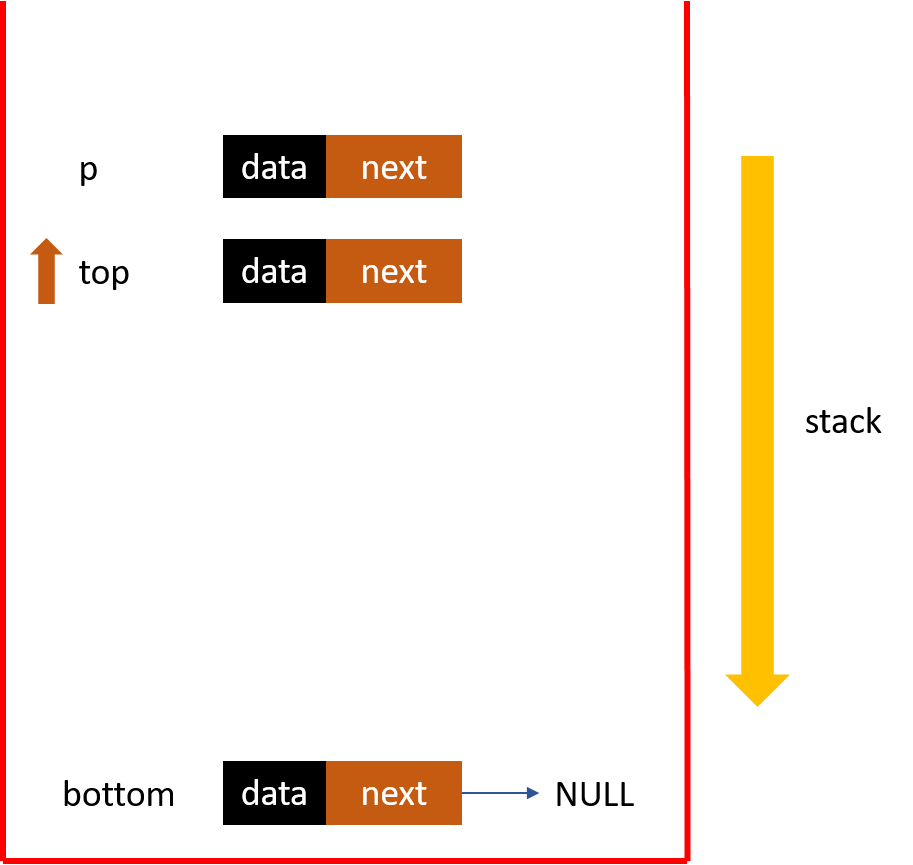
stack

顺序栈

链共享

链栈

Reference:

typedef - creates an alias that can be used anywhere in place of a (possibly complex) type name.

走进数据结构和算法（c++版）（4）——栈

This pic helps me better understand linked stack:

【算法】表达式求值–逆波兰算法介绍

中缀表达式转换为后缀表达式
你需要设定一个栈SOP,和一个线性表 L 。SOP用于临时存储运算符和分界符( ，L用于存储后缀表达式。
遍历原始表达式中的每一个表达式元素
（1）如果是操作数，则直接追加到 L中。只有运算符或者分界符（才可以存放到栈SOP中
（2）如果是分界符
Ⅰ 如果是左括号 ( ，则直接压入SOP，等待下一个最近的右括号与之配对。
Ⅱ 如果是右括号），则说明有一对括号已经配对(在表达式输入无误的情况下)。不将它压栈，丢弃它，然后从SOP中出栈，得到元素e，将e依次追加到L里。一直循环，直到出栈元素e 是左括号 ( ，同样丢弃他。
（3）如果是运算符（用op1表示）
Ⅰ如果SOP栈顶元素（用op2表示）不是运算符，则二者没有可比性，则直接将此运算符op1压栈。例如栈顶是左括号 ( ，或者栈为空。
Ⅱ 如果SOP栈顶元素（用op2表示）是运算符，则比较op1和 op2的优先级。如果op1 > op2 ，则直接将此运算符op1压栈。
如果不满足op1 > op2，则将op2出栈，并追加到L，重复步骤3。
也就是说，如果在SOP栈中，有2个相邻的元素都是运算符，则他们必须满足：下层运算符的优先级一定小于上层元素的优先级，才能相邻。

最后，如果SOP中还有元素，则依次弹出追加到L后，就得到了后缀表达式。

Reverse Polish notation

for each token in the postfix expression:
  if token is an operator:
    operand_2 ← pop from the stack
    operand_1 ← pop from the stack
    result ← evaluate token with operand_1 and operand_2
    push result back onto the stack
  else if token is an operand:
    push token onto the stack
result ← pop from the stack

How to convert infix notation into postfix notation

create an empty array to fill in operands, an empty stack to fill in operators and delimiter
if operands true, add it into array
if delimiter true:

a. if delimiter means left parenthesis, push it into stack

b. if delimiter means right parenthesis, pop it out of stack until it meets first left parenthesis, ends.
if read infix notation from left to right and meets operator (denoted as op1), and now the top of the stack is already a operator type (denoted as op2)

a. if the priority of op1 > op2, push op1 into stack

b. if the priority of op1 <= op2, pop out op1 into array
finally, if finish reading full infix notation, the stack is still has some elements, then follow the FILO rule to pop them out and add them respectively into the array to generate the final postfix notation